26. Новогодние подарки
Деду Морозу и Снегурочке нужно
доставить n подарков детям.
Зная время t1 упаковки каждого подарка Снегурочкой и время его
доставки Дедом Морозом t2,
вычислить наименьшее время, необходимое для выполнения всех заказов. В свой
мешок Дед Мороз может положить только один подарок.
Вход. В первой
строке находится количество подарков n
(1 ≤ n ≤ 300). В
следующих двух строках содержится по n
чисел, соответственно: во второй строке – время упаковки каждого подарка
Снегурочкой, а в третьей – время его доставки Дедом Морозом. Известно, что 0
< t1, t2 ≤ 1000.
Выход. Наименьшее
время доставки всех подарков.
|
Пример входа |
Пример выхода |
|
5 4 4
30 6 2 5 1
4 30 3 |
47 |
РЕШЕНИЕ
жадный алгоритм
Анализ алгоритма
Это классическая
задача про два станка, которые последовательно обрабатывают детали.
Пусть время
упаковки i-го подарка Снегурочкой
равно ai, а время
его доставки Дедом Морозом равно bi. Ищем наименьшее значение среди чисел ai
и bi (i = 1, n). Если наименьшим значением
будет ai, то ставим i - ый подарок на обработку
первым, если bi – то последним. После этого удаляем i
- ый подарок из списка. Повторяем описанный процесс для оставшихся (n –
1)-го подарка.
Отметим,
что подарок не может быть доставлен Дедом морозом пока он не будет упакован
Снегурочкой. Если Деду Морозу доступно несколько подарков для доставки, которые
уже упакованы Снегурочкой, то будем пользоваться следующим правилом: порядки
упаковки подарков Снегурочкой и доставки Дедом Морозом должны совпадать.
Пример
Рассмотрим
работу алгоритма на примере, приведённом в условии задачи:
|
4 |
4 |
30 |
6 |
2 |
|
5 |
1 |
4 |
30 |
3 |
Начало
очереди и её окончание имеют соответственно номера 1 и 5. Первый локальный
минимум обеих массивов равен 1 и находится во втором массиве, поэтому ставим
подарок № 2 в конец очереди на выполнение работ, то есть на место 5 (меняем
местами подарки под номерами 2 и 5):
|
4 |
2 |
30 |
6 |
4 |
|
5 |
3 |
4 |
30 |
1 |
При этом
найденный подарок номер два из дальнейшего рассмотрения исключаем, что
аналогично тому, что мы уменьшим на единицу номер хвоста очереди, он теперь
равен 4. Ищем новый локальный минимум в обеих массивах, он равен 2 и находится
в первом массиве, поэтому ставим подарок № 2 (мы ведь поменяли этот подарок на
предыдущем шаге с каким-то) в начало очереди на выполнение работ, соответственно
меняем подарки 1 и 2 местами, и увеличиваем начало очереди:
|
2 |
4 |
30 |
6 |
4 |
|
3 |
5 |
4 |
30 |
1 |
Среди
оставшихся подарков с номера 2 по 4 ищем новый локальный минимум. Он находится в первом массиве, поэтому ставим
его в начало очереди на выполнение работ, а начало очереди увеличиваем на
единицу, оно станет равно 3:
|
2 |
4 |
30 |
6 |
4 |
|
3 |
5 |
4 |
30 |
1 |
Новый
локальный минимум 4 находится во втором массиве, поэтому ставим его в конец
очереди:
|
2 |
4 |
6 |
30 |
4 |
|
3 |
5 |
30 |
4 |
1 |
Соответственно
мы при этом уменьшили номер хвоста рассматриваемого списка до 3, номер начала и
хвоста рассматриваемой очереди совпали, поэтому алгоритм сортировки на этом
заканчивает свою работу, но не заканчивается алгоритм решения задачи. Далее
нужно аккуратно посчитать полученное суммарное время, ибо 2-й исполнитель (Дед
Мороз) не может отвезти подарок раньше, чем Снегурочка (1-й исполнитель)
закончит его упаковку.
Перейдём к
подсчёту суммарного затраченного времени. Очевидно, что для минимизации временных
затрат 1-й исполнитель должен работать непрерывно, пока не упакует все подарки,
после чего сможет отдохнуть. Также очевидно, что второй исполнитель не сможет
приступить к доставке очередного подарка, пока он не упакован первым
исполнителем, поэтому ему точно придётся дождаться окончания упаковки 1-го
подарка и далее, возможно, придётся также дожидаться окончания упаковки
очередного подарка в сформированной ранее очереди выполнения работ. Весь этот
процесс графически изображен на рисунке ниже.
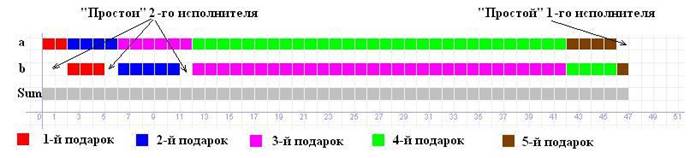
Обозначим через sum наименьшее время доставки всех подарков. Тогда если, например,
имеется только один подарок, то sum =
a1+ b1. В случае двух подарков sum = a1+ max(a2, b1) + b2.
Реализация алгоритма
Ячейка v[i] вектора пар будет хранить время
упаковки i-го подарка Снегурочкой и
время его доставки Дедом Морозом.
vector<pair<int,int> > v;
int up[310];
Функция
сравнения cmp, согласно которой сортируются пары в векторе v. Неравенство a < b должно иметь место, если либо минимум достигается на a.first (тогда подарок а ставим в начало), либо на b.second (тогда подарок b ставим в конец).
int cmp(pair<int,int> a,
pair<int,int>
b)
{
int mm =
min(min(a.first,a.second),min(b.first,b.second));
if ((mm == a.first) || (mm == b.second)) return 0;
return 1;
}
Реализуем
собственную функцию сортировки обменом.
void sort(void)
{
int i, j;
for(i = 0; i < v.size(); i++)
for(j = i + 1; j < v.size(); j++)
if (cmp(v[i],v[j])) swap(v[i],v[j]);
}
Основная
часть программы. Читаем входные данные, заполняем массив пар v.
scanf("%d",&n);
for(i = 0; i < n; i++) scanf("%d",&up[i]);
for(i = 0; i < n; i++)
scanf("%d",&b),
v.push_back(make_pair(up[i],b));
Сортируем
вектор v.
sort();
Вычисляем
минимальное время доставки всех подарков и выводим ответ. На i-ой итерации переменная sum содержит наименьшее время доставки
первых i подарков.
for(a = sum = i = 0; i < v.size();
i++)
a += v[i].first, sum
= max(a,sum) + v[i].second;
printf("%d\n",sum);